Network Modeling with the Infinite Relational Model¶

The Enron e-mail corpus contains 500,00 emails between 150 individuals at Enron. To analyze the communication network, we created a binary matrix to represent email communication between individuals.

In this matrix, \(X_{i,j} = 1\) if and only if person\(_{i}\) sent an email to person\(_{j}\) Note that we are only recording if an email was ever sent, not the number of emails. Thus our resulting matrix is a binary matrix.

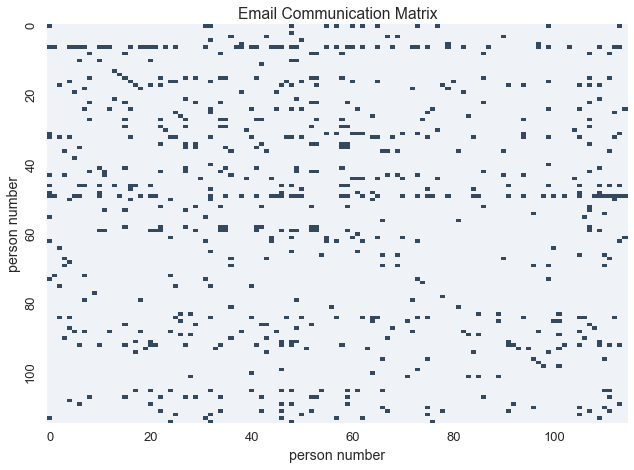
We’d like to learn what the different classes of people are in the Enron dataset. Maybe some people (like salespeople) sent a lot of e-mails outside of the company, and some people (like HR) only sent e-mails to people inside of the company. Maybe some people received a lot of e-mail (like bosses) and others received virtually none. We’ll learn the underlying clusters in this communication matrix using the Inifinite Relational Model. In this model, the underlying clusters represents groups of indiviudals in the network based on the kinds of who they email.

The domain of our model is the individuals in the email dataset.

Our relations are emails between individuals, both of cardinality \(N\), and we model the relation with beta-bernoulli distribution since our data is binary

defn = model_definition([N], [((0, 0), beta_bernoulli)])
views = [numpy_dataview(communications_relation)]
prng = rng()

We initialize our model and run a large number of samplers – one per CPU core.

nchains = cpu_count()
latents = [model.initialize(defn, views, r=prng, cluster_hps=[{'alpha':1e-3}]) for _ in xrange(nchains)]
kc = runner.default_assign_kernel_config(defn)
runners = [runner.runner(defn, views, latent, kc) for latent in latents]
r = parallel.runner(runners)

From here, we can finally run each chain of the sampler 1000 times

start = time.time()
r.run(r=prng, niters=1000)
print "inference took {} seconds".format(time.time() - start)

Now that we have learned our model let’s get our cluster assignments

infers = r.get_latents()
clusters = groups(infers[0].assignments(0), sort=True)
ordering = list(it.chain.from_iterable(clusters))

Let’s sort the communications matrix to highlight our inferred clusters

z = communications_relation.copy()
z = z[ordering]
z = z[:,ordering]
sizes = map(len, clusters)
boundaries = np.cumsum(sizes)[:-1]

Our model finds suspicious cluster based on the communication data. We’ll color and label these clusters in our communications matrix.

def cluster_with_name(clusters, name, payload=None):
    ident = namemap[name]
    for idx, cluster in enumerate(clusters):
        if ident in cluster:
            return idx, (cluster, payload)
    raise ValueError("could not find name")

suspicious = [
    cluster_with_name(clusters, "horton-s", {"color":"#66CC66", "desc":"The pipeline/regulatory group"}),


    cluster_with_name(clusters, "skilling-j", {"color":"#FF6600", "desc":"The VIP/executives group"}),
]
suspicious = dict(suspicious)

for idx, (boundary, size) in enumerate(zip(boundaries, sizes)):
    if size < 5:
        continue
    plt.plot(range(N), boundary*np.ones(N), color='#0066CC')
    plt.plot(boundary*np.ones(N), range(N), color='#0066CC')
    if idx in suspicious:
        rect = patches.Rectangle((boundary-size, boundary-size),
            width=size, height=size, alpha=0.5, fc=suspicious[idx][1]["color"])
        plt.gca().add_patch(rect)
plt.imshow(z, cmap=blue_cmap, interpolation='nearest', aspect='auto')
@savefig email_matrix_colored.png width=5in

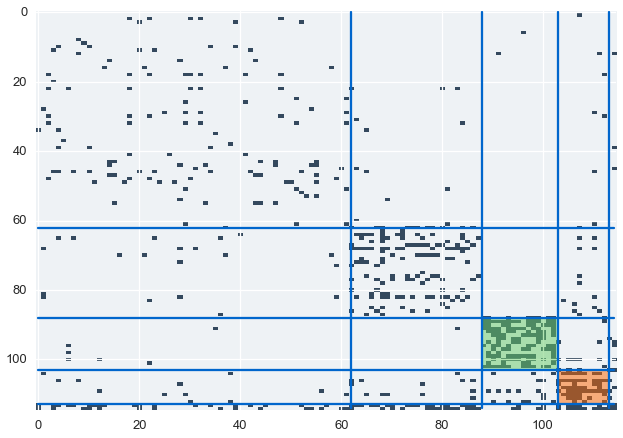
We’ve identified two suspicious clusters. Let’s look at the data to find out who these individuals are

def cluster_names(cluster):
    return [names[idx] for idx in cluster]
def get_full_name(name):
    return enron_utils.FULLNAMES.get(name, name)
def get_title(name):
    return enron_utils.TITLES.get(name, "?")

for cluster, payload in suspicious.values():
    cnames = cluster_names(cluster)
    ctitles = map(get_title, cnames)
    print payload["desc"]
    for n, t in zip(cnames, ctitles):
        print "\t", get_full_name(n), '\t\t"{}"'.format(t)
    print

The pipeline/regulatory group
    Lynn Blair              "?"
    Shelley Corman          "Vice President Regulatory Affairs"
    Lindy Donoho            "Employee"
    Drew Fossum             "Vice President"
    Tracy Geaccone          "Employee"
    harris-s                "?"
    Rod Hayslett            "Vice President Also Chief Financial Officer and Treasurer"
    Stanley Horton          "President Enron Gas Pipeline"
    Kevin Hyatt             "Director Pipeline Business"
    Michelle Lokay          "Employee Administrative Asisstant"
    Teb Lokey               "Manager Regulatory Affairs"
    Danny McCarty           "Vice President"
    mcconnell-m             "?"
    Darrell Schoolcraft             "?"
    Kimberly Watson                 "?"

The VIP/executives group
    Rick Buy                "Manager Chief Risk Management Officer"
    Jeff Dasovich           "Employee Government Relation Executive"
    David Delainey          "CEO Enron North America and Enron Enery Services"
    Louise Kitchen          "President Enron Online"
    John Lavorato           "CEO Enron America"
    Richard Shapiro                 "Vice President Regulatory Affairs"
    Jeffery Skilling                "CEO"
    Barry Tycholiz          "Vice President"
    Greg Whalley            "President"
    williams-j              "?"

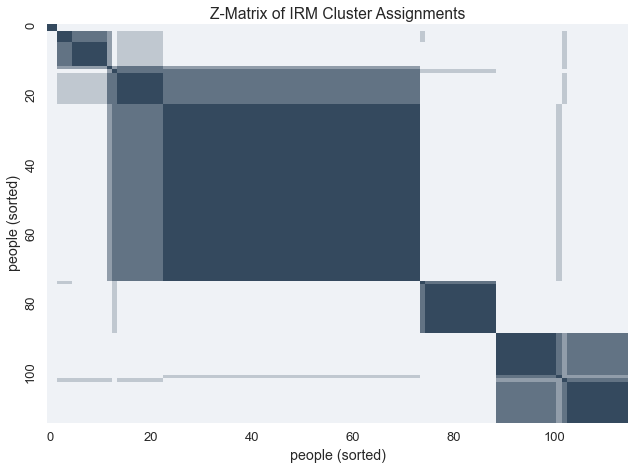
Given the uncertainty behind these latent clusters, we can visualize the variablity within these assignments with a z-matrix. Ordering the z-matrix allows us to group members of each possible cluster together.

zmat = query.zmatrix(domain=0, latents=infers)
zmat = zmatrix_reorder(zmat, zmatrix_heuristic_block_ordering(zmat))
sns.heatmap(zmat, cmap=blue_cmap, cbar=False, xticklabels=labels, yticklabels=labels)
plt.xlabel('people (sorted)')
plt.ylabel('people (sorted)')
plt.title('Z-Matrix of IRM Cluster Assignments')
@savefig zmatrix.png width=5in

To cluster network data using datamicroscopes, the IRM is available for installation from conda

$ conda install microscopes-irm